Soal UTS Strategi Algoritma

Contoh Soal UTS Strategi Algoritma UAD

PROGRAM STUDI TEKNIK INFORMATIKA UNIVERSITAS AHMAD DAHLAN

Mata Kuliah           : Strategi Algoritma Hari/Tanggal          : Waktu Ujian          :

Dosen     : E. Haodudin Nurkifli Sifat        :

1.    Menganalisis Algoritma  [30]

algoritma Bubble Sort

procedure BubbleSort (input/output L : TabelInt, input n : integer) {      Mengurutkan tabel L[1..N] sehingga terurut menaik dengan metode pengurutan bubble sort.   Masukan : Tabel L yang sudah terdefenisi nilai-nilainya.   Keluaran: Tabel L yang terurut menaik sedemikian sehingga                 L[1] £ L[2] £ … £ L[N].  }

Deklarasi    i    : integer     { pencacah untuk jumlah langkah }    k    : integer     { pencacah,untuk pengapungan pada setiap langkah }    temp : integer     { peubah bantu untuk pertukaran }

Algoritma:    for i ¬ 1 to n - 1 do      for k ¬  n downto i + 1 do         if L[k] < L[k-1] then           {pertukarkan L[k] dengan L[k-1]}            temp ¬  L[k]            L[k] ¬  L[k-1]            L[k-1] ¬ temp          endif      endfor         endfor

Jika ada larik L dengan 10 buah elemen yang berisi angka-angka yang random :

7	10	16	13	4	12	3	81	75	26
1	2	3	4	5	6	7	8	9	10

a.        Tulislah Proses dari algoritma bubble sort di atas  sampai di capai angka yang terurut ?.

b.       Tentukan waktu terbaik (T_min) dan waktu terburuk (T_max)  dari Algoritma Bubble Sort di atas ? (pada saat kondisi seperti apa Bubble Sort di katakana mencapai waktu terbaik dan pada kondisi seperti apa BubbleSort di katakana mencapai waktu terburuk).

2.    Greedy Algoritma Huffman Code [40]

Algotima Huffman encoding -------------------------------------------------------------------------- INPUT : urutkan list dari node binary tree (t1,t2,....tn) dari alfabet (S1, S2, .....Sn) dengan frekuensi (W1,W2,.....,Wn) OUTPUT : Huffman Code 1.  inisialisasi list dari node binary tree (t1,t2,....tn) diambil dari ukuran frekuensinya (W1,W2,.....,Wn) 2. for k = 1; k < n; k = k + 1 do 3. ambil dua pohon misalkan ti dan tj yang  mempunyai ukuran yang    minimal (wi<=wj) 4. t <-- gabungkan (ti,tj) dengan ukuran w = wi + wj    dimana anak_kiri (t)<--ti dan anak_kanan (t)<--tj 5. edge(t,ti)<--0; edge(t,tj)<--1 6. endfor

Jika ada string “ Harta Karun Di Bawah Lantai ” dengan menggunakan algoritma Huffman code di atas tentukan hasil code Huffman tersebut ? (Spasi diabaikan)

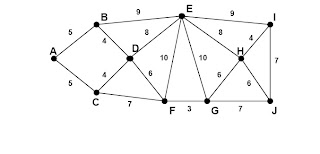
3.    Algoritma Minimum Spanning Tree (MST) [30]

a.     Buatlah MST dengan Algoritma Kruskal dan tuliskan algoritmanya pada Graph di bawah ?

b.     Buatlah MST dengan Algoritma Prim’s dan tuliskan algoritmanya Graph di bawah ?